Лента Мёбиуса

Эта статья находится на начальном уровне проработки, в одной из её версий выборочно используется текст из источника, распространяемого под свободной лицензией
Материал из энциклопедии Руниверсалис
У этого термина существуют и другие значения, см. Лист Мёбиуса (значения).
Лента Мёбиуса
Римская мозаика III века нашей эры с изображением кольца, свернутого как лента Мёбиуса, мюнхенская Глиптотека

Ле́нта Мёбиуса (лист Мёбиуса, петля́ Мёбиуса) — топологический объект, простейшая неориентируемая поверхность с краем, односторонняя при вложении в обычное трёхмерное евклидово пространство [math]\displaystyle{ \R^3 }[/math].

Считается, что лента Мёбиуса была открыта независимо немецкими математиками Августом Фердинандом Мёбиусом и Иоганном Бенедиктом Листингом в 1858 году, хотя похожая структура изображена на римской мозаике III века нашей эры[1][2].

Модель ленты Мёбиуса можно легко сделать: надо взять достаточно длинную бумажную полоску и склеить противоположные концы полоски в кольцо, предварительно перевернув один из них. В трёхмерном евклидовом пространстве существуют два типа полос Мёбиуса в зависимости от направления закручивания: правые и левые.

Эйлерова характеристика листа Мёбиуса равна нулю.

Уравнения

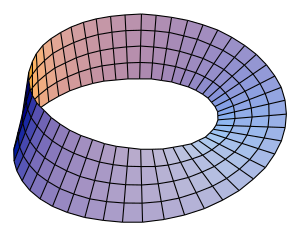
Параметрическое описание листа Мёбиуса
Чтобы превратить квадрат в лист Мёбиуса, соедините края, помеченные буквой A, так, чтобы направления стрелок совпали

Одним из способов представления листа Мёбиуса как подмножества [math]\displaystyle{ \R^3 }[/math] является параметризация:

[math]\displaystyle{ x \left( u, v \right) = \left( 1 +\frac {v} {2} \cos\frac {u} {2} \right) \cos u, }[/math]
[math]\displaystyle{ y \left( u, v \right) = \left( 1 +\frac {v} {2} \cos\frac {u} {2} \right) \sin u, }[/math]
[math]\displaystyle{ z \left( u, v \right) = \frac {v} {2} \sin\frac {u} {2}, }[/math]

где [math]\displaystyle{ 0\leqslant u \lt 2\pi }[/math] и [math]\displaystyle{ -1\leqslant v\leqslant 1 }[/math]. Эти формулы задают ленту Мёбиуса ширины 1, чья центральная окружность имеет радиус 1, лежит в плоскости [math]\displaystyle{ xy }[/math] с центром в [math]\displaystyle{ \left( 0,\;0,\;0 \right) }[/math]. Параметр [math]\displaystyle{ u }[/math] пробегает вдоль ленты, а [math]\displaystyle{ v }[/math] задает расстояние от края.

В цилиндрических координатах [math]\displaystyle{ \left( r,\;\theta,\;z \right) }[/math] неограниченная версия листа Мёбиуса может быть представлена уравнением:

[math]\displaystyle{ \log r \sin \frac{\theta}{2} = z \cos \frac{\theta}{2}, }[/math]

где логарифм имеет произвольное основание.

Свойства

  • Граница листа Мёбиуса состоит из одной замкнутой кривой.
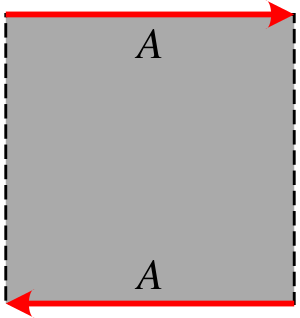
  • Топологически лист Мёбиуса может быть определён как факторпространство квадрата [math]\displaystyle{ \left[ 0,\;1 \right] \times \left[ 0,\;1 \right] }[/math] по отношению эквивалентности [math]\displaystyle{ \left( x,\;0 \right) \sim \left( 1-x,\;1 \right) }[/math] для [math]\displaystyle{ 0\leqslant x\leqslant 1 }[/math].
  • Лист Мёбиуса — это также пространство нетривиального расслоения над окружностью со слоем отрезок.
  • Ленту Мёбиуса возможно поместить в [math]\displaystyle{ \R^3 }[/math] с границей, являющейся идеальной окружностью. Один из способов — применить стереографическую проекцию к бутылке Клейна, погруженной в трёхмерную сферу. Идея состоит в следующем: пусть [math]\displaystyle{ C }[/math] будет единичным кругом в плоскости [math]\displaystyle{ xy }[/math] в [math]\displaystyle{ \R^3 }[/math]. Соединив антиподные точки на [math]\displaystyle{ C }[/math] (то есть точки под углами [math]\displaystyle{ \theta }[/math] и [math]\displaystyle{ \theta + \pi }[/math]) дугой круга, получим, что для [math]\displaystyle{ \theta }[/math] между [math]\displaystyle{ 0 }[/math] и [math]\displaystyle{ \pi/2 }[/math] дуги лежат выше плоскости [math]\displaystyle{ xy }[/math], а для других [math]\displaystyle{ \theta }[/math] — ниже (причём в двух местах дуги лежат в плоскости [math]\displaystyle{ xy }[/math]).[источник не указан 3103 дня]
    • Тем не менее любой диск, который приклеивается к граничной окружности, неизбежно пересечёт ленту Мёбиуса.
  • Примером вложения листа Мебиуса в [math]\displaystyle{ \Complex^2 }[/math] является поверхность, заданная уравнением
[math]\displaystyle{ z_1 = \sin\eta\,e^{i\varphi} }[/math]
[math]\displaystyle{ z_2 = \cos\eta\,e^{i\varphi/2}, }[/math]
Здесь параметр [math]\displaystyle{ \eta }[/math] изменяется от 0 до [math]\displaystyle{ \pi }[/math]. Границей этой поверхности является окружность [math]\displaystyle{ z_1 = 0, |z_2| = 1 }[/math]. При стереографической проекции получается вложение в [math]\displaystyle{ \R^3 }[/math] с границей, в точности являющейся окружностью.

Открытые вопросы

  1. Каково минимальное [math]\displaystyle{ k }[/math] такое, что из прямоугольника с меньшей стороной 1 и большей стороной k можно свернуть несамопересекающуюся ленту Мёбиуса (бумагу мять не разрешается)? Доказанная оценка снизу — [math]\displaystyle{ \frac{\pi}{2} }[/math], сверху — [math]\displaystyle{ \sqrt 3 }[/math][3].
  2. Существует ли формула, описывающая лист Мёбиуса, получающийся путём складывания плоского листа бумаги? Вышеуказанные формулы описывают поверхность, которую нельзя сложить из листа бумаги, так как она имеет отрицательную кривизну; спрашивается, можно ли аналогичным образом описать поверхность нулевой кривизны?[4]
    • Сложнее найти форму, которая при этом минимизирует упругую энергию изгиба. Решение этой задачи, впервые поставленной Садовским (M. Sadowsky) в 1930 году, было опубликовано в 2007 году[5]. Однако решение не описывается алгебраической формулой, и маловероятно, что такая формула вообще существует. Чтобы найти пространственную равновесную форму бумажной ленты Мёбиуса, необходимо решить краевую задачу для системы дифференциально-алгебраических уравнений[en].

Если ленту разрезать

Разрезание ленты Мёбиуса по линии, которая отстоит от краёв на треть ширины
  • Если разрезать ленту вдоль по линии, равноудалённой от краёв, вместо двух лент Мёбиуса получится одна длинная двусторонняя (закрученная на полный оборот) лента. Это свойство ленты Мёбиуса используется в старинном фокусе под названием «афганские ленты»[6] (англ. The Afghan Bands) с 1904 года[7], его также описывают Норберт Винер в книге I Am a Mathematician (1956)[8] и Мартин Гарднер в книге Mathematics, Magic and Mystery (1956), последний также утверждает, что самая ранняя ссылка на использование ленты Мёбиуса для фокусов относится к 1882 году[9]. Если получившуюся ленту разрезать вдоль посередине, получаются две такие ленты, намотанные друг на друга.
  • Если разрезать ленту Мёбиуса, отступая от края приблизительно на треть её ширины, то получаются две ленты, одна — более короткая лента Мёбиуса, другая — длинная лента с двумя полуоборотами[10].
  • Другие комбинации лент могут быть получены из лент с двумя или более полуоборотами в них. Например, если разрезать ленту с тремя полуоборотами, то получится лента, завитая в узел трилистника. Разрез ленты с дополнительными оборотами даёт неожиданные фигуры, названные парадромными кольцами.

Искусство и технология

Международный символ переработки представляет собой лист Мёбиуса
«Лента Мёбиуса» над входом в институт ЦЭМИ РАН (1976, архитектор Леонид Павлов, художники Э. А. Жаренова и В. К. Васильцов)

Лист Мёбиуса служил вдохновением для скульптур и для графического искусства. Эшер был одним из художников, кто особенно любил его и посвятил несколько своих литографий этому математическому объекту. Одна из известных — «Лист Мёбиуса II»[11], показывает муравьёв, ползающих по поверхности ленты Мёбиуса.

Лист Мёбиуса является эмблемой серии научно-популярных книг «Библиотечка „Квант“». Он также постоянно встречается в научной фантастике, например, в рассказе Артура Кларка «Стена мрака». Иногда научно-фантастические рассказы (вслед за физиками-теоретиками) предполагают, что наша Вселенная может быть некоторым обобщённым листом Мёбиуса. Также кольцо Мёбиуса постоянно упоминается в произведениях уральского писателя Владислава Крапивина, цикл «В глубине Великого Кристалла» (например, «Застава на Якорном Поле. Повесть»). В рассказе «Лист Мёбиуса» автора А. Дж. Дейча, бостонское метро строит новую линию, маршрут которой становится настолько запутанным, что превращается в ленту Мёбиуса, после чего на этой линии начинают исчезать поезда. По мотивам рассказа был снят фантастический фильм «Мёбиус» режиссёра Густаво Москера. Также идея ленты Мёбиуса используется в рассказе М. Клифтона «На ленте Мёбиуса».

В 1987 году советский джазовый пианист Леонид Чижик записал альбом «Лента Мёбиуса», в который вошла и одноимённая композиция.

Существуют технические применения ленты Мёбиуса. Полоса ленточного конвейера, выполненная в виде ленты Мёбиуса, будет работать дольше, потому что вся поверхность ленты изнашивается равномерно. Также в системах записи на непрерывную плёнку применяются ленты Мёбиуса (чтобы удвоить время записи). Во многих матричных принтерах красящая лента также имеет вид ленты Мёбиуса для увеличения её ресурса.

Также над входом в институт ЦЭМИ РАН находится мозаичный горельеф «Лента Мёбиуса» работы архитектора Леонида Павлова[12] в соавторстве с художниками Э. А. Жареновой и В. К. Васильцовым (1976)[13].

Иногда считается, что лента Мёбиуса является прообразом символа бесконечности [math]\displaystyle{ \infty }[/math], однако последний появился на два века раньше[14].

Вариации и обобщения

  • Близкой односторонней поверхностью является бутылка Клейна. Бутылка Клейна может быть получена путём склеивания двух лент Мёбиуса по краям. В обычном трёхмерном евклидовом пространстве сделать это, не создавая самопересечения, невозможно.
  • Другое похожее многообразие — проективная плоскость. Если проколоть отверстие в проективной плоскости, тогда то, что останется, будет листом Мёбиуса. С другой стороны, если приклеить диск к ленте Мёбиуса, совмещая их границы, то результатом будет проективная плоскость.

См. также

Примечания

  1. ↑ Larison, Lorraine L. (1973). «The Möbius band in Roman mosaics». American Scientist 61 (5): 544–547. Bibcode: 1973AmSci..61..544L.
  2. ↑ (2016) «Möbius strips before Möbius: topological hints in ancient representations». The Mathematical Intelligencer 38 (2): 69–76. arXiv:1609.07779. doi:10.1007/s00283-016-9631-8. Bibcode: 2016arXiv160907779C.
  3. ↑ Фукс Д. Лента Мёбиуса. Вариации на старую тему Архивная копия от 15 ноября 2011 на Wayback Machine // «Квант», № 1, 1979.
  4. ↑ Randrup T., Rogen P. Sides of the Möbius strip (англ.) // Archiv der Mathematik : journal. — 1996. — Vol. 66. — P. 511—521.
  5. ↑ Starostin. E. L., van der Heijden G. H. M. The shape of a Möbius strip (англ.) // Nature Materials : journal. — 2007. — doi:10.1038/nmat1929.
  6. ↑ Гарднер М. Профессор, у которого не было ни одной стороны. Примечания автора // Наука и жизнь. — 1977. — № 5. — С. 127.
  7. ↑ Professor Hoffmann. Later Magic. — New York, London: E. P. Dutton & Company, George Routledge & Sons, 1904. — P. 471—473.
  8. ↑ Norbert Wiener. I Am a Mathematician. — Garden City, New York: Doubleday & Company, 1956. — P. 26—27. В русском переводе: Норберт Винер. Я — математик / Пер. с англ. Ю. С. Родман. — 2-е изд. — М.: Наука, 1967. — С. 19—20.
  9. ↑ Martin Gardner. Mathematics, Magic and Mystery. — New York: Dover Publications, 1956. — P. 70—73.
  10. ↑ Кордемский Б. А. Топологические опыты своими руками Архивная копия от 8 июня 2016 на Wayback Machine // «Квант», № 3, 1974
  11. ↑ M.C. Escher — Möbius Strip II. Дата обращения: 5 октября 2014. Архивировано 6 октября 2014 года.
  12. ↑ Мастер вычисления. Дата обращения: 12 декабря 2015. Архивировано 22 декабря 2015 года.
  13. ↑ Архитектор Мария Серова — о «доме с ухом» Леонида Павлова — The Village — The Village. Дата обращения: 12 декабря 2015. Архивировано 22 декабря 2015 года.
  14. ↑ Лента Мёбиуса // Журнал «Weekend» № 10 (106) от 20.03.2009. Дата обращения: 4 августа 2012. Архивировано 4 августа 2012 года.

Литература

  • Фоменко А. Т., Фукс Д. Б. Курс гомотопической топологии.— М.: Наука, 1989.
  • Гарднер М. Математические чудеса и тайны.— М.: Наука, 1978.

Ссылки

Источник — https://xn--h1ajim.xn--p1ai/index.php?title=Лента_Мёбиуса&oldid=5819035